本文讲解了矩阵乘法的两种视角。

矩阵乘法的两种视角

矩阵

$$
\mathbf{A} =
\begin{pmatrix}
{a}_{11} & {a}_{12} & \cdots & {a}_{1m}
\\
{a}_{21} & {a}_{22} & \cdots & {a}_{2m}
\\
\vdots & \vdots & \ddots & \vdots
\\
{a}_{n1} & {a}_{n2} & \cdots & {a}_{nm}
\end{pmatrix}
\in \mathbb{R}^{n \times m}
, \quad
\mathbf{B} =
\begin{pmatrix}
{b}_{11} & {b}_{12} & \cdots & {b}_{1k}
\\
{b}_{21} & {b}_{22} & \cdots & {b}_{2k}
\\
\vdots & \vdots & \ddots & \vdots
\\
{b}_{m1} & {b}_{n2} & \cdots & {b}_{mk}
\end{pmatrix}
\in \mathbb{R}^{m \times k}
$$
$$
\mathbf{C} =
\mathbf{A} \cdot \mathbf{B}
$$
$$
\mathbf{C}
\in \mathbb{R}^{n \times k}
$$

视角1：行乘列

$$
\mathbf{A} =
\begin{pmatrix}
\mathbf{a}_{1} & \mathbf{a}_{2} & \cdots & \mathbf{a}_{m}
\end{pmatrix}
, \quad
\mathbf{a}_{i} =
\begin{pmatrix}
{a}_{1i}
\\
{a}_{2i}
\\
\vdots
\\
{a}_{ni}
\end{pmatrix}
\in \mathbb{R}^{n \times 1}
$$
$$
\mathbf{B} =
\begin{pmatrix}
\mathbf{b}_{1}
\\
\mathbf{b}_{2}
\\
\vdots
\\
\mathbf{b}_{m}
\end{pmatrix}
, \quad
\mathbf{b}_{i} =
\begin{pmatrix}
{b}_{i1} & {b}_{i2} & \cdots & {b}_{ik}
\end{pmatrix}
\in \mathbb{R}^{1 \times k}
$$
$$
\mathbf{C} =
\mathbf{A} \cdot \mathbf{B} =
\begin{pmatrix}
\mathbf{a}_{1} & \mathbf{a}_{2} & \cdots & \mathbf{a}_{m}
\end{pmatrix}
\cdot
\begin{pmatrix}
\mathbf{b}_{1}
\\
\mathbf{b}_{2}
\\
\vdots
\\
\mathbf{b}_{m}
\end{pmatrix} =
\sum\limits_{i = 1}^{m}
\mathbf{a}_{i}
\cdot
\mathbf{b}_{i}
$$
$$
\mathbf{C} =
\sum\limits_{i = 1}^{m}
\begin{pmatrix}
{a}_{1i}
\\
{a}_{2i}
\\
\vdots
\\
{a}_{ni}
\end{pmatrix}
\cdot
\begin{pmatrix}
{b}_{i1} & {b}_{i2} & \cdots & {b}_{ik}
\end{pmatrix}
=
\sum\limits_{i = 1}^{m}
\begin{pmatrix}
{a}_{1i}\cdot{b}_{i1} & {a}_{1i}\cdot{b}_{i2} & \cdots & {a}_{1i}\cdot{b}_{ik}
\\
{a}_{2i}\cdot{b}_{i1} & {a}_{2i}\cdot{b}_{i2} & \cdots & {a}_{2i}\cdot{b}_{ik}
\\
\vdots & \vdots & \ddots & \vdots
\\
{a}_{ni}\cdot{b}_{i1} & {a}_{ni}\cdot{b}_{i2} & \cdots & {a}_{ni}\cdot{b}_{ik}
\end{pmatrix}
$$

视角2：列乘行

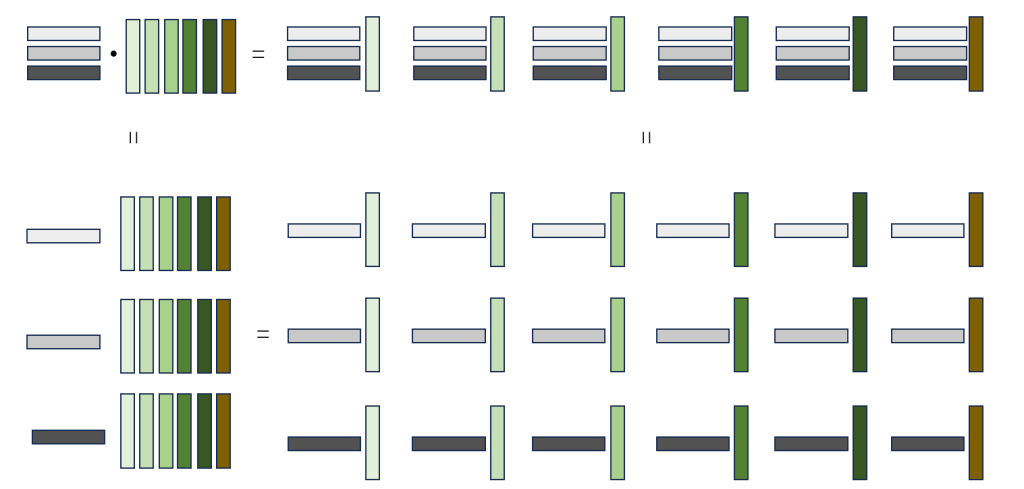
$$
\mathbf{A} =
\begin{pmatrix}
\mathbf{a}_{1}
\\
\mathbf{a}_{2}
\\
\vdots
\\
\mathbf{a}_{n}
\end{pmatrix}
, \quad
\mathbf{a}_{i} =
\begin{pmatrix}
{a}_{i1} & {a}_{i2} & \cdots & {a}_{im}
\end{pmatrix}
\in \mathbb{R}^{1 \times m}
$$
$$
\mathbf{B} =
\begin{pmatrix}
\mathbf{b}_{1} & \mathbf{b}_{2} & \cdots & \mathbf{b}_{k}
\end{pmatrix}
, \quad
\mathbf{b}_{i} =
\begin{pmatrix}
{b}_{1i}
\\
{b}_{2i}
\\
\vdots
\\
{b}_{mi}
\end{pmatrix}
\in \mathbb{R}^{m \times 1}
$$
$$
\mathbf{C} =
\mathbf{A} \cdot \mathbf{B} =
\begin{pmatrix}
\mathbf{a}_{1}
\\
\mathbf{a}_{2}
\\
\vdots
\\
\mathbf{a}_{n}
\end{pmatrix}
\cdot
\begin{pmatrix}
\mathbf{b}_{1} & \mathbf{b}_{2} & \cdots & \mathbf{b}_{k}
\end{pmatrix} =
\begin{pmatrix}
\mathbf{a}_{1}\cdot\mathbf{b}_{1} & \mathbf{a}_{1}\cdot\mathbf{b}_{2} & \cdots & \mathbf{a}_{1}\cdot\mathbf{b}_{k}
\\
\mathbf{a}_{2}\cdot\mathbf{b}_{1} & \mathbf{a}_{2}\cdot\mathbf{b}_{2} & \cdots & \mathbf{a}_{2}\cdot\mathbf{b}_{k}
\\
\vdots & \vdots & \ddots & \vdots
\\
\mathbf{a}_{n}\cdot\mathbf{b}_{1} & \mathbf{a}_{n}\cdot\mathbf{b}_{2} & \cdots & \mathbf{a}_{n}\cdot\mathbf{b}_{k}
\end{pmatrix}
$$
$$
\mathbf{C} =
\begin{pmatrix}
\begin{pmatrix}
{a}_{11} & {a}_{12} & \cdots & {a}_{1m}
\end{pmatrix}
\cdot
\begin{pmatrix}
{b}_{11}
\\
{b}_{21}
\\
\vdots
\\
{b}_{m1}
\end{pmatrix}
&
\cdots
&
\begin{pmatrix}
{a}_{11} & {a}_{12} & \cdots & {a}_{1m}
\end{pmatrix}
\cdot
\begin{pmatrix}
{b}_{1k}
\\
{b}_{2k}
\\
\vdots
\\
{b}_{mk}
\end{pmatrix}
\\
\vdots & \ddots & \vdots
\\
\begin{pmatrix}
{a}_{n1} & {a}_{n2} & \cdots & {a}_{nm}
\end{pmatrix}
\cdot
\begin{pmatrix}
{b}_{11}
\\
{b}_{21}
\\
\vdots
\\
{b}_{m1}
\end{pmatrix}
&
\cdots
&
\begin{pmatrix}
{a}_{n1} & {a}_{n2} & \cdots & {a}_{nm}
\end{pmatrix}
\cdot
\begin{pmatrix}
{b}_{1k}
\\
{b}_{2k}
\\
\vdots
\\
{b}_{mk}
\end{pmatrix}
\end{pmatrix}
$$
$$
\mathbf{C} =
\begin{pmatrix}
\sum\limits_{i = 1}^{m}
{a}_{1i}\cdot{b}_{i1}
&
\sum\limits_{i = 1}^{m}
{a}_{1i}\cdot{b}_{i2}
&
\cdots
&
\sum\limits_{i = 1}^{m}
{a}_{1i}\cdot{b}_{ik}
\\
\sum\limits_{i = 1}^{m}
{a}_{2i}\cdot{b}_{i1}
&
\sum\limits_{i = 1}^{m}
{a}_{2i}\cdot{b}_{i2}
&
\cdots
&
\sum\limits_{i = 1}^{m}
{a}_{2i}\cdot{b}_{ik}
\\
\vdots
&
\cdots
&
\ddots
&
\vdots
\\
\sum\limits_{i = 1}^{m}
{a}_{ni}\cdot{b}_{i1}
&
\sum\limits_{i = 1}^{m}
{a}_{ni}\cdot{b}_{i2}
&
\cdots
&
\sum\limits_{i = 1}^{m}
{a}_{ni}\cdot{b}_{ik}
\end{pmatrix}
$$