摘要
数据集压缩(dataset condensation),亦称数据集蒸馏(dataset distillation),旨在通过对数据集进行压缩以求减少模型训练的工作量或者说是提升学习过程的效率。比较直观的方法即是匹配真实数据集批次与合成数据集批次之间的梯度来实现上述的数据集压缩过程,但是这个方式由于其对于整体的忽视可能会导致主要梯度偏差较大的过拟合结果。本文将介绍一种2022年提出的利用特征对齐来压缩数据集的方法$^{[1]}$,该方法保留了真实特征分布(real-feature distribution)以及合成数据集的判别能力,从而使其在各种架构中都有强大的泛化能力。方法核心是一种在多尺度对齐两集特征的同时也考虑原数据集的真实样本分类的有效策略。此外,本方法以利用新颖的动态双层优化来自适应地调整参数以避免欠拟合与过拟合。本方法比起此前的方法在一些数据集上的表现更加优秀,比方说在SVHN数据集上性能提升了11%。
背景介绍
虽然近年来深度神经网络(deep neural networks, DNNs)在计算机视觉(computer vision)领域的应用是令人兴奋的,但随之而来的是人们对于模型训练成本挂钩于消耗庞大算力资源的海量数据集的担忧。因此,研究人员开始尝试通过构建小型的训练集来简化繁琐的训练过程,其中最经典的方法即使通过构建核心数据集(coreset),然而这个NP-难问题使其在大规模的数据集的计算上难以处理,因而更多诉诸于启发式的贪心算法(greedy algorithms)权衡最优性来加快流程。
数据集压缩,亦称数据集蒸馏,作为一种自2018年提出后快速发展的概念,旨在通过转化真实数据集为一个更小的合成数据集来实现模型训练效果的等价从而提升训练的效率。回顾这个领域过去的一些研究,2018年开创性地提出了基于元学习(meta-learning)的策略,由于其嵌套循环优化(nestloop optimization)带来的复杂度问题使其无法扩展到更大规模的数据集中$^{[2]}$。而在之后2021年的的报道中,人们通过强制性地最小化合成集中批量样本的梯度与真实集中的梯度距离来绕开了递归计算$^{[3]}$。不过梯度匹配的方法还是具有两个缺点,首先由于深度神经网络的记忆效应会对产生主导梯度的困难样本或者噪声印象深刻,从而可能忽略那些具有代表性但是简单的样本进而造成过拟合。此外,不同神经网络架构对于困难样本的梯度响应彼此间并不相同,如果只是依赖于梯度匹配的方法的话,会导致学到的合成数据偏向少数不具代表性的数据点,因此对陌生架构的泛化能力较差。
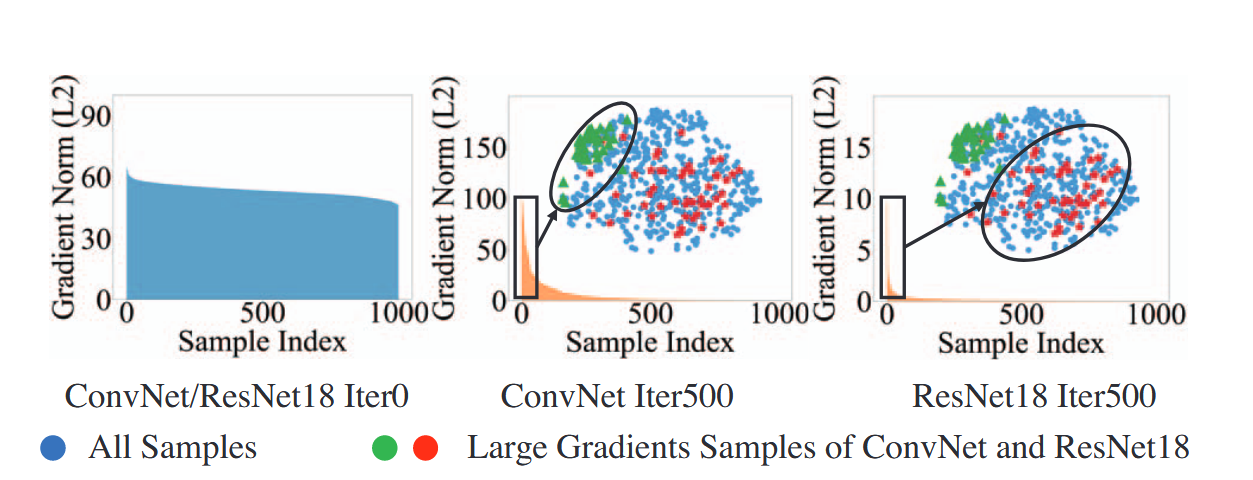

如图1a展示了不同的深度神经网络架构中的困难样本,即大梯度样本,分布情况重叠很小,说明如果对于陌生架构可能泛化能力并不强;梯度分布也从初期的均匀分布到后期的长尾分布,即可能产生高度偏向性。如图1b展示了以ConvNet架构为例的梯度匹配方法与本文的特征对齐方法之间的合成集在真实集上的分布差异散点图,可以看到利用特征对齐的方法可以更好地让合成集去代表真实集。
为了解决批次梯度匹配带来的学习偏差问题,文章提出了一种利用特征对齐的方法来实现数据集的压缩。该方法通过应用分布级的监督匹配两集中涉及中间层的特征从而注意到尽可能所有的样本以求两集的分布一致性,从而减小了因架构不同导致的困难样本差异化造成的泛化能力降低的影响。
在具体的CAFE方法之中还有两个要点值得一看,首先是采用了两种互补的损失函数分别关注不同方面的内容,一方面为了实现两集的分布匹配,因此逐层的强制特征对齐要求获取数据分布的信息,保证两集数据的多尺度特征一致性;另外一个方面,考虑到合成集的判别能力,还要基于真实样本之于合成簇(sythetic clustsers)的亲和力进行分类,并以其结果定义第二个损失函数,从而实现合成集的判别能力学习,增强不同类别特征的可区分性。其次,CAFE还使用动态优化策略,即应用了新颖的双层优化方案从而可以自定义随机梯度下降(stochastic gradient descent, SGD)方法中的步数来更新网络与合成集数据。并以此弥补了此前工作欠拟合与过拟合的问题。
核心方法
如图2中可以看到CAFE方法中最核心的三个模块:逐层特征对齐、判别损失、动态双层优化。第一个模块用于获取真实数据集的精确分布信息、第二个模块用于发掘判别样本的判别损失、第三个模块用于减少欠拟合和过拟合对合成集数据的影响。
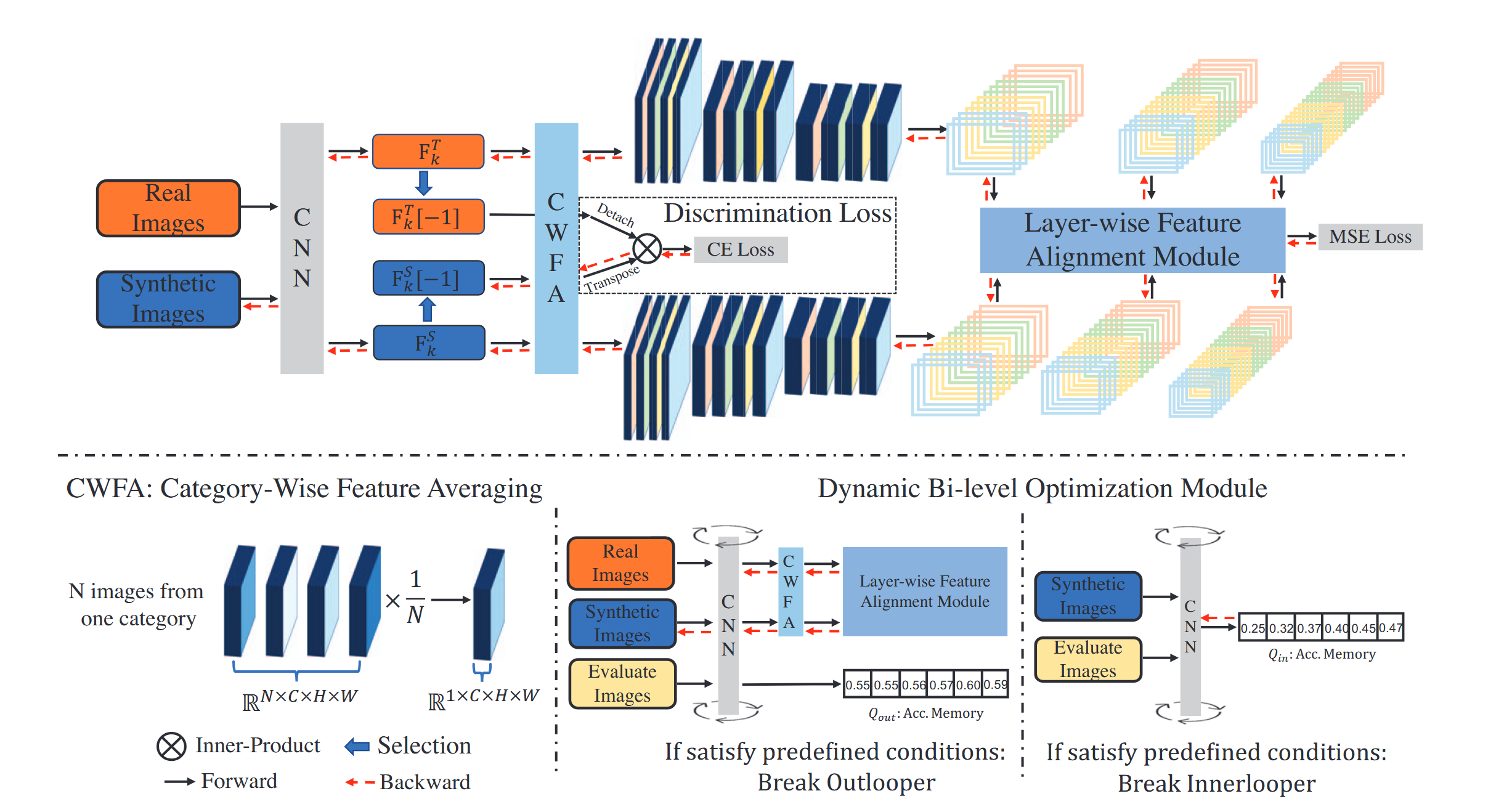
逐层特征对齐(layer-wise features alignment)
该模块的核心是通过依类特征平均(category-wise feature averaging, CWFA)简化真实数据集$\mathcal{T}$与合成数据集$\mathcal{S}$在每一卷积层以及每一类之间的特征差异,随后将这种差异利用平均平方误差(mean square error. MSE)约束逐层逐类最后对类与层求和构造$\mathcal{T}$与$\mathcal{S}$的特征分布匹配损失函数$\mathcal{L}_\mathrm{f}$来实现两集的特征逐层对齐。
- 依类采集样本$$
\begin{align}\mathcal{T}_k\in\mathbb{R}^{N\times{C}\times{H}\times{W}}\newline\mathcal{S}_k\in\mathbb{R}^{M\times{C}\times{H}\times{W}}\end{align}
$$
其中$N$与$M$分别是$\mathcal{T}_k$与$\mathcal{S}_k$的依类采样批次的样本数,即样本维度,$C$代表通道数(channels),$H$代表图像的高度(height),$W$代表图像的宽度(width),因此最终采集样本被表示为一个四维张量。 - 网络提层级特征
利用神经网络$\phi_\theta(\cdot)$逐层提取特征$$
\begin{align}{F}^\mathcal{T}_{k}=[{f}^\mathcal{T}_{k,1},{f}^\mathcal{T}_{k,2},\dots,{f}^\mathcal{T}_{k,L}]=\phi_\theta(\mathcal{T}_{k})\newline{F}^\mathcal{S}_{k}=[{f}^\mathcal{S}_{k,1},{f}^\mathcal{S}_{k,2},\dots,{f}^\mathcal{S}_{k,L}]=\phi_\theta(\mathcal{S}_{k})\end{align}
$$
其中第$l$层的特征可以被表示为${f}^\mathcal{T}_{k,l}\in\mathbb{R}^{N\times{C}\times{H}\times{W}}$与${f}^\mathcal{S}_{k,l}\in\mathbb{R}^{M\times{C}\times{H}\times{W}}$ - 样本维度特征压缩
特征平均的关键步骤就是对张量进行样本维度的平均$$
\begin{align}{f}^\mathcal{T}_{k,l}\in\mathbb{R}^{N\times{C}\times{H}\times{W}}\to\bar{f}^\mathcal{T}_{k,l}\in\mathbb{R}^{1\times{C}\times{H}\times{W}}\newline{f}^\mathcal{S}_{k,l}\in\mathbb{R}^{M\times{C}\times{H}\times{W}}\to\bar{f}^\mathcal{S}_{k,l}\in\mathbb{R}^{1\times{C}\times{H}\times{W}}\end{align}
$$ - 损失函数计算$$
\begin{align}\mathcal{L}_\mathrm{f}=\sum^{K}_{k=1}{\sum^{L}_{l=1}{\vert{\bar{f}^\mathcal{S}_{k,l}-\bar{f}^\mathcal{T}_{k,l}}\vert^2}}\end{align}
$$
其中$K$和$L$分别代表数据集中的类别数和卷积的层数(不包括输出层)
判别损失(discrimination loss)
为了弥补只考虑特征分布造成的判别性样本挖掘的缺失,总损失函数的构建还需要判别损失的介入。判别性样本(discrimination sample)通常指的是那些处于分类边界的的对于分类有着显著性影响的样本。$\mathcal{S}$应该被视为$\mathcal{T}$的一种分类器,因而这个模块对最后一层的特征进行操作。
- 提取特征
判别损失计算用到的数据是最后一层的特征,因此我们需要取$\mathcal{S}$中的$\bar{f}^{\mathcal{S}}_{k,L}\in\mathbb{R}^{1\times{C}\times{H}\times{W}}$并且将其拼接成新的向量$\bar{F}^{\mathcal{S}}_{L}=[\bar{f}^{\mathcal{S}}_{1,L},\bar{f}^{\mathcal{S}}_{2,L},\dots,\bar{f}^{\mathcal{S}}_{K,L}]$,而在对应的$\mathcal{T}$中则直接取真实数据组成向量${F}^{\mathcal{T}}_{L}=[{f}^{\mathcal{T}}_{1,L},{f}^{\mathcal{T}}_{2,L},\dots,{f}^{\mathcal{T}}_{K,L}]$,这里之所以使用的真实集的特征与合成集的平均特征,可能是出于三方面的考虑:减少噪声增强鲁棒性、简化计算、捕捉类别的全局信息 - 分类逻辑的计算
$\mathcal{T}$中的样本分类依靠于两个向量之间的内积计算(向量的相似度可以用内积衡量,结果越大,特征越相似,从而可用于分类)$$
\begin{align}\mathbf{O}=\langle{F}^{\mathcal{T}}_L,(\bar{F}^{\mathcal{S}}_L)^{\mathtt{T}}\rangle\end{align}
$$
其中$\mathbf{O}\in\mathbb{R}^{{N’}\times{K}}$包含着$N’=K\times{N}$个真实数据点 - 分类损失的计算
通过$softmax$函数计算每个样本类别概率$$
\begin{align}p_i=softmax(\mathbf{O}_i)\end{align}
$$
再根据所有样本的类别概率依照交叉熵损失计算判别损失$\mathcal{L}_{\mathtt{d}}$$$
\begin{align}\mathcal{L}_{\mathtt{d}}=-\frac{1}{N’}\sum^{N’}_{i=1}{\mathtt{log}p_i}\end{align}
$$ - 构建总的损失函数并优化
总的损失函数$\mathcal{L}_{\mathtt{total}}$可以通过两个模块的损失函数共同构建,并且最终通过优化总损失函数获得合成数据集的参数。$$
\begin{align}\mathcal{L}_{\mathtt{total}}={\mathcal{L}_{\mathtt{f}}}+{\beta}{\mathcal{L}_{\mathtt{d}}}\newline\mathcal{S}\leftarrow\mathop{\arg\min}\limits_{\mathcal{S}}\mathcal{L}_{\mathtt{total}}\end{align}
$$
其中$\beta$是判别损失函数的正数权重。
动态双层优化(dynamic bi-level optimization)
双层优化虽然并非完全新颖的东西,但是这里还是起到了很好的优化作用。这是一种嵌套优化,外层更新合成数据集$\mathcal{S}$内层更新模型的参数$\theta$目标是使合成数据集能够泛化到不同的模型参数$\theta$,从而提升其鲁棒性和泛化能力。
传统的双层优化固定步数,可能导致过拟合或欠拟合,且调参成本过高,通过监控模型在查询集(query set)上的性能,自动决定何时停止内层优化或更新$\mathcal{S}$,查询集是一个随机取样真实数据集样本构成的评估优化模型性能的集合,根据内层优化$\theta$后模型在其上表现的变化来决定是否跳出内优化。而$\lambda_1$与$\lambda_2$是两个性能不敏感的动态优化超参数。整体算法如算法1所示。

实验结果
以下是实验中涉及到的数据集:MNIST、FashionMNIST、SVHN、CIFAR10/100
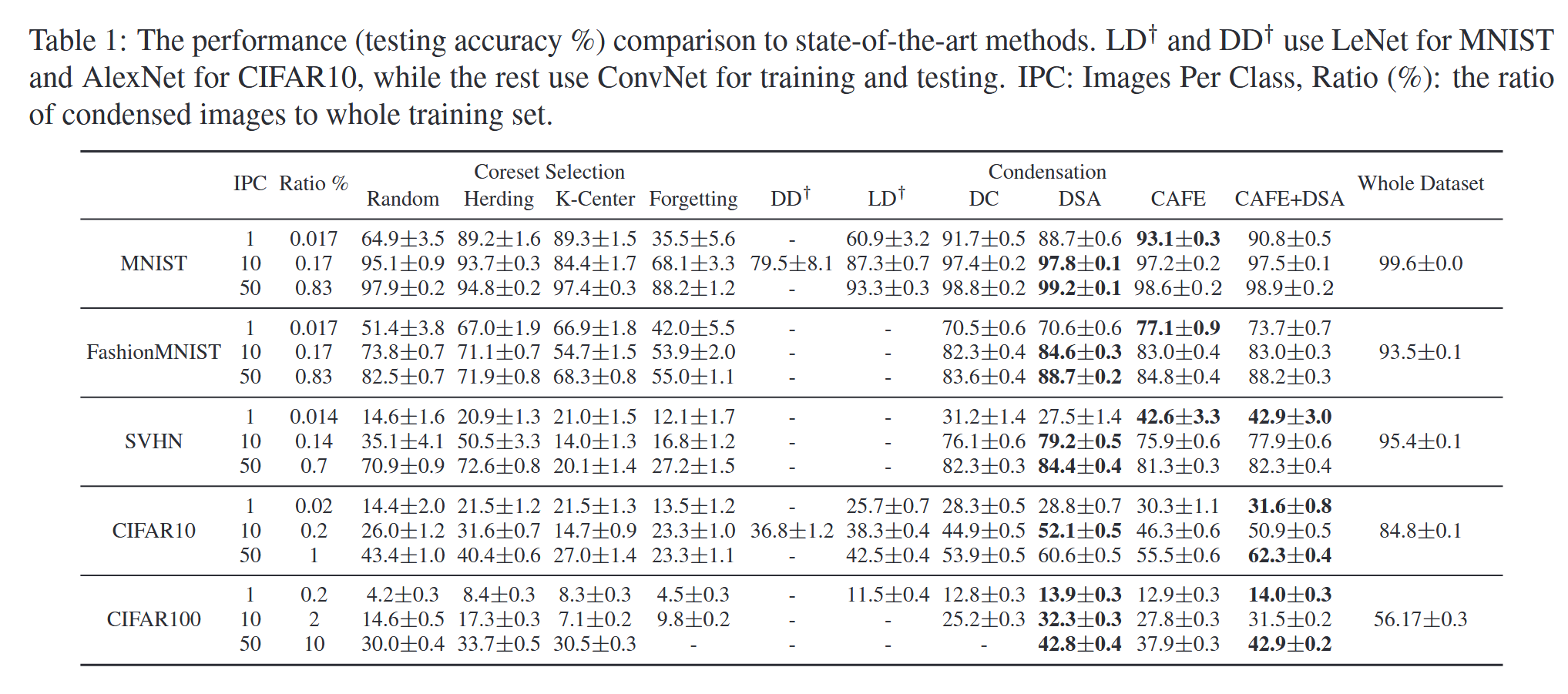
文章中将CAFE与两大类方法进行了比较,分别是核心数据集选择与数据集蒸馏,前者包括Random$^{[4]}$,Herding$^{[5]}$,K-Center$^{[6]}$,Forgetting$^{[7]}$等方法,后者包括了DD$^{[2]}$,LD$^{[8]}$,DC$^{[3]}$,DSA$^{[9]}$等数据集蒸馏的具体方法。在上述五个数据集上进行实验对比,结果如表1所示,主要有以下几个点值得关注:
5. 每类1张图片(IPC=1)时,CAFE性能最佳,在SVHN和FashionMNIST上分别比其他方法提升了11%和6.5%,DD类方法明显优于前一类,核心数据集选择类方法中,Herding与K-Center优于Random与Forgetting。
6. 每类10张图片(IPC=10)与每类50张图片(IPC=50)时,比起DC方法在大多数数据集上提升了0.7%~2.6%,在CIFAR10/100上与DSA方法表现相当或略优。
此外,如表2所示消解实验的结果表明在三个模块中,最重要的还是逐层特征对齐,其次是判别损失与动态双层优化,三者均对方法的表现有贡献。

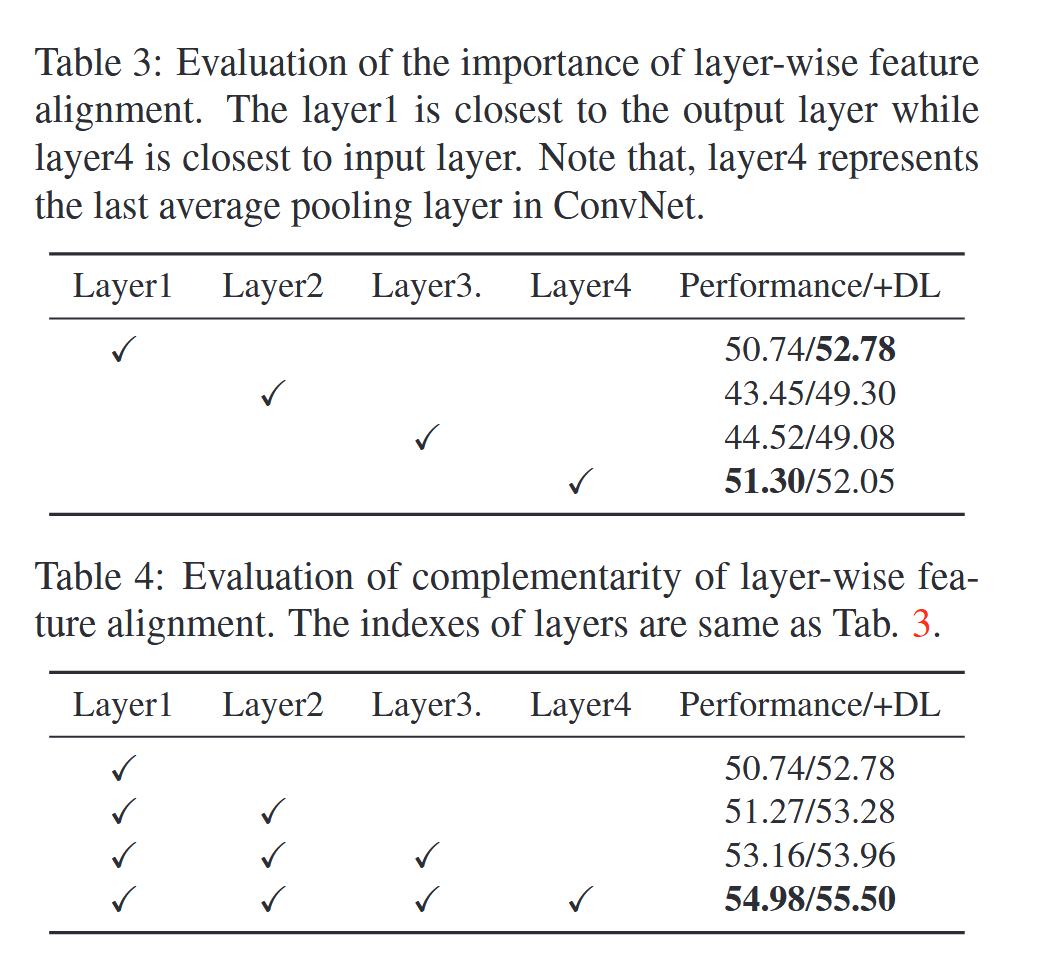
而其他的消解实验如表3表4所示,说明了逐层对齐的重要性,而其中对齐第一层与第四层尤为关键,其中如果加入了判别损失那么性能也会得到提升,而随着多一层特征对齐的增加可以明显看到性能整体呈每层约1%的上升趋势。
而对于方法中涉及到的三个超参数的研究结果如图3所示,整体上方法对动态优化超参不敏感,损失函数的判别损失权重则取1时最佳。
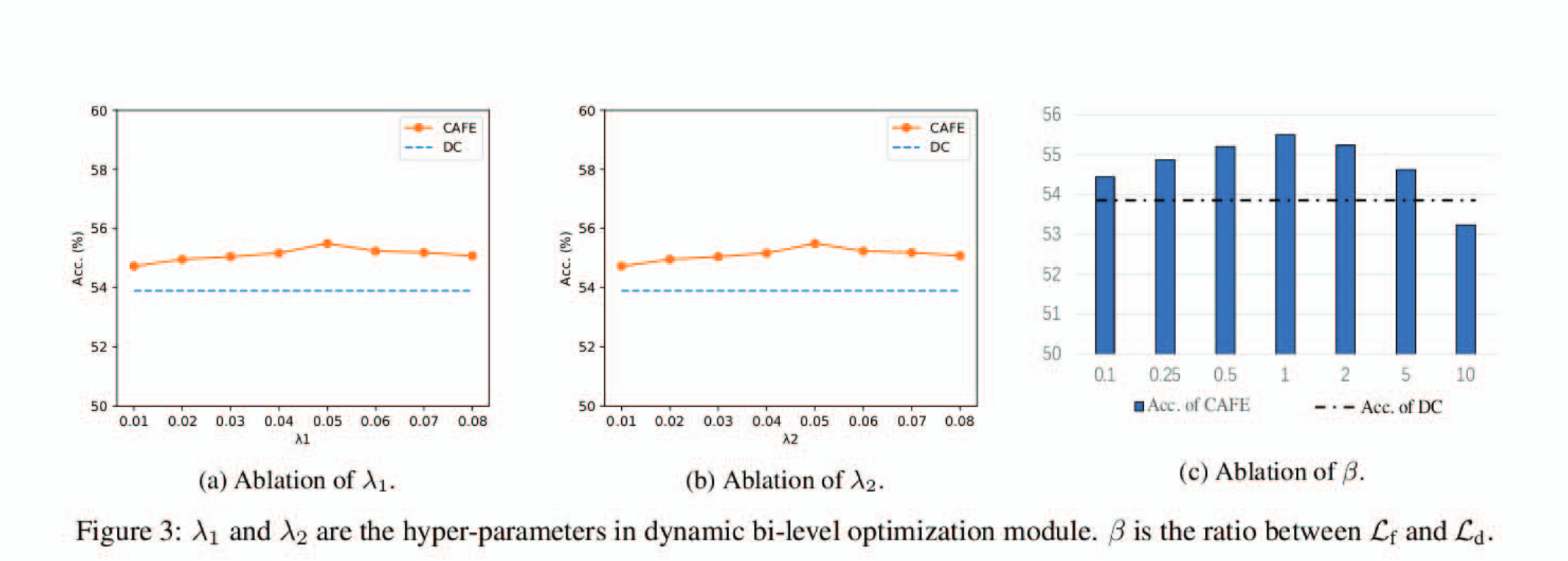
在动态双层优化中,与查询集优化模型参数相关的队列大小$\gamma$也是一个超参数,如表5所示当其为10时准确率最佳且消耗时间远小于DC$^{[3]}$方法。

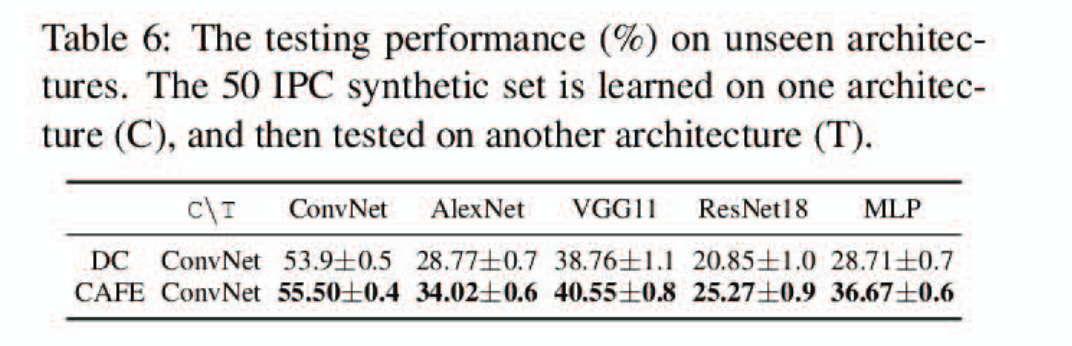
最后,在表6中可以看到,同样利用ConvNet网络压缩得到合成数据集,CAFE方法在同架构乃至不同架构上的训练表现均要优于DC$^{[3]}$方法。
如图4图5所示,通过图片以及散点图分布等可视化的信息可以看到,CAFE比起DC方法生成的合成数据集更加具有与原集的视觉相似性,且语义信息更丰富清晰度更高,散点图分布显示CAFE能够更好地去均匀地体现原集的分布,具有更强的代表性。


总结
总结来说,这篇文献提出了一种新颖的数据集压缩方法CAFE,通过逐层特征对齐、判别损失和动态双层优化三大模块,有效保留真实数据集的分布特征和判别能力,使其在陌生架构上具有强大的泛化能力。实验表明,CAFE 在多个数据集上性能优于现有技术,且计算成本更低,适用于实际场景。
参考文献
$[1]$ Wang, K.; Zhao, B.; Peng, X.; Zhu, Z.; Yang, S.; Wang, S.; Huang, G.; Bilen, H.; Wang, X.; You, Y. CAFE: Learning to Condense Dataset by Aligning Features. In 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR); 2022; pp 12186–12195. https://doi.org/10.1109/CVPR52688.2022.01188.
$[2]$ Wang, T.; Zhu, J.-Y.; Torralba, A.; Efros, A. A. Dataset Distillation. arXiv February 24, 2020. https://doi.org/10.48550/arXiv.1811.10959.
$[3]$ Zhao, B.; Mopuri, K. R.; Bilen, H. Dataset Condensation with Gradient Matching. arXiv March 8, 2021. https://doi.org/10.48550/arXiv.2006.05929.
$[4]$Chen, Y.; Welling, M.; Smola, A. Super-Samples from Kernel Herding. arXiv March 15, 2012. https://doi.org/10.48550/arXiv.1203.3472.
$[5]$Belouadah, E.; Popescu, A. ScaIL: Classifier Weights Scaling for Class Incremental Learning. arXiv January 16, 2020. https://doi.org/10.48550/arXiv.2001.05755.
$[6]$Sener, O.; Savarese, S. Active Learning for Convolutional Neural Networks: A Core-Set Approach. arXiv June 1, 2018. https://doi.org/10.48550/arXiv.1708.00489.
$[7]$Toneva, M.; Sordoni, A.; Combes, R. T. des; Trischler, A.; Bengio, Y.; Gordon, G. J. An Empirical Study of Example Forgetting during Deep Neural Network Learning. arXiv November 15, 2019. https://doi.org/10.48550/arXiv.1812.05159.
$[8]$Bohdal, O.; Yang, Y.; Hospedales, T. Flexible Dataset Distillation: Learn Labels Instead of Images. arXiv December 12, 2020. https://doi.org/10.48550/arXiv.2006.08572.
$[9]$Zhao, B.; Bilen, H. Dataset Condensation with Differentiable Siamese Augmentation. arXiv June 10, 2021. https://doi.org/10.48550/arXiv.2102.08259.


